Motion-Planning学习记录_23spring
一、实验任务
RRT的衍生算法的仿真实现
熟悉掌握常见的地图搜索算法 RRT 的拓展算法:
- RRT*: 引入成本函数的概念,通过重新连接已有节点,以寻求更优的路径
- Informed RRT*: 引入启发式信息指导树的生长方向,以提高搜索效率
- Dynamic RRT: 根据环境特征动态调整节点扩展的步长,提升算法在复杂环境中的 性能
二、实验步骤
2.1 RRT算法
RRT(Rapidly-Exploring Random Trees)是一种基于随机采样的路径规划算法,采用增量式采样的搜索方法。将其应用于路径规划时无需事先对环境信息进行处理和存储,具有较好的适应性,适用于解决复杂环境以及多种约束条件的路径规划问题。
算法主要流程是以空间中的起始点作为根节点,在空间中利用增量方式进行随机采样,然后向外延伸扩展以增加叶节点。重复该步骤直到获得一棵从起点到目标点的树,最后通过回溯找到从根节点到目标点的无碰撞路径。
RRT 算法的优点包括不需要启发式函数、能够快速规划出一条安全路径,适用于复杂环境和多种约束条件的路径规划问题。然而,它也存在一些缺点:稳定性不佳、内存消耗较大、效率相对较低、路径可能存在曲折冗余点以及无法有效检测动态障碍物等问题。
具体流程为:
- 初始化:算法初始时,只包含起点作为根节点的树。
- 随机采样:每次迭代,算法在整个搜索空间中随机采样生成节点,用于扩展树并搜索路径。
- 最近节点:计算树中所有节点到随机节点的距离,找到最近的节点作为最近节点。
- 扩展新节点:从最近节点朝向随机节点的方向扩展出一个新节点,准确来说,是沿着从最近节点到随机节点的连线方向拓展,沿着这个连线移动一个固定的步长,得到新节点的位置。
- 碰撞检测:在将新节点添加到树中之前,算法会检查从最近节点到新节点的路径段是否与任何障碍物发生碰撞。如果没有碰撞,则新节点会被添加到树中。
- 检查目标:检查新节点是否与终点足够接近。如果新节点与终点足够接近,则尝试直接连接到终点。如果连接成功且无碰撞,算法结束,找到了一条路径。
- 重复迭代:重复步骤 2-6,直到找到路径或达到预定的迭代次数。
以下是 RRT 中最核心的三个函数:
2.1.1 plan 函数
这是算法的核心执行函数,其目标是通过迭代生成随机节点,并将其与最近的树节点连接,然后检查新节点是否与障碍物发生碰撞。如果新节点是安全的,则将其添加到树中。算法会持续执行直到找到一条达到终点的路径或达到最大迭代次数为止。
1 | def plan(self): |
2.1.2 generateRandomNode函数
按照一定概率采样,随机生成一个节点,小于目标采样率就直接返回目标节点。
1 | def generateRandomNode(self) -> Node: |
2.1.3 getNearest函数
用于寻找已有点中和当前随机点最近的点,并基于该最近节点扩展出一个新的节点,决定了如何从探索树中选择最佳的节点进行扩展,以生成新的节点用于路径搜索。
1 | def getNearest(self, node_list: list, node: Node) -> Node: |
2.2 RRT* 算法
RRT算法只关注于快速找到一条从起点到终点的路径,而不保证路径的最优性;而且由线段连接成的路径不光滑,不太适合机器人去执行。
RRT* 是对 RRT 算法的优化,引入了成本函数的概念,并通过重新连接已有节点以寻求更优的路径,通过评估和优化路径成本,确保最终找到的路径是最优或接近最优的。
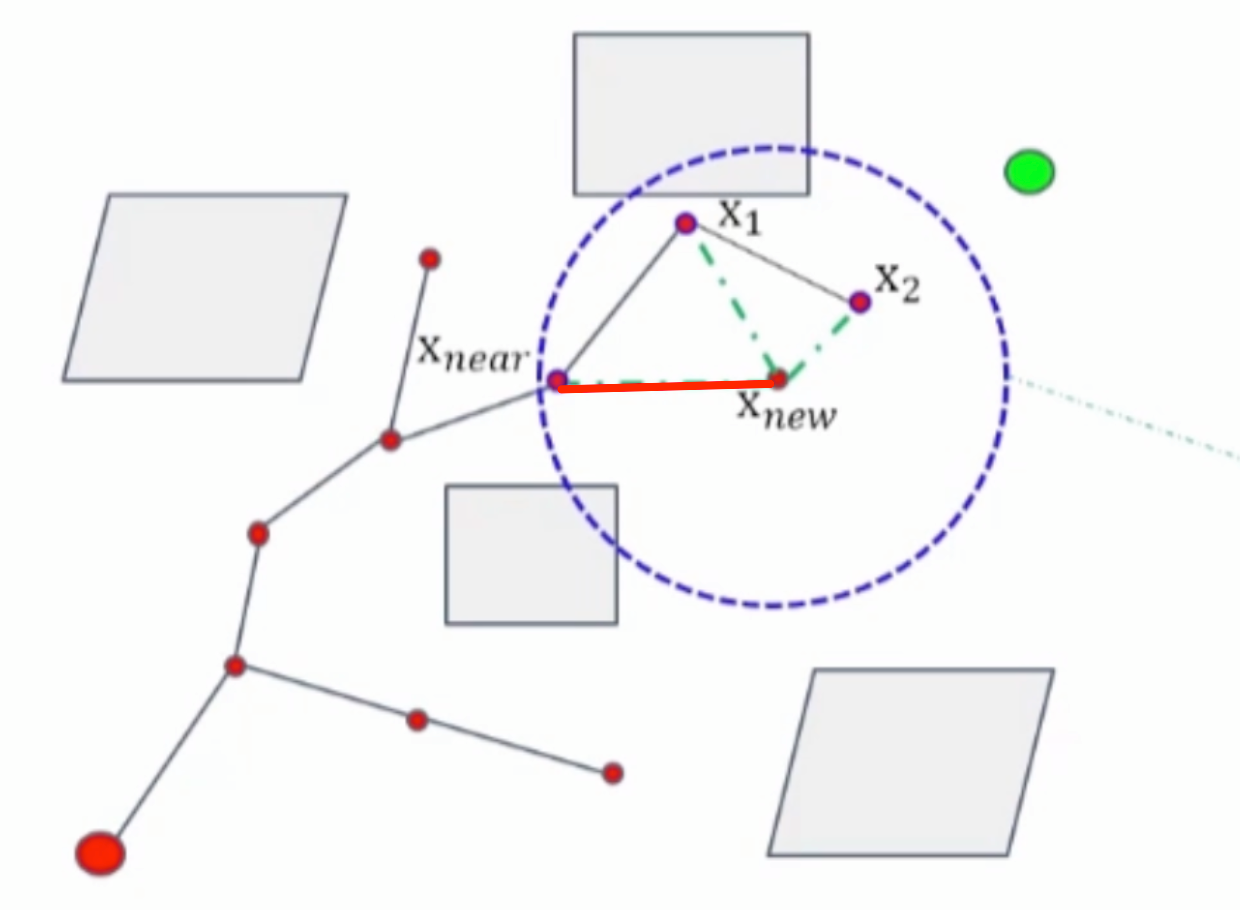
算法流程与RRT算法流程基本相同,不同之处主要在于在RRT当中,找到 Xnew 之后是与Xnear 直接相连的,但是在 RRT* 当中,找到了 Xnew 之后,就会在 Xnew 之间找到一个范围,在这个范围内,画一个以R为半径的圆,继续搜索其他的点。
这时把找到的多个节点都通过直线连接起来,下一步用动态规划的思想,选择这些点中 Cost 最小的点:
以上这个过程也叫重布线,其意义在于每当生成了新的节点后,判断是否可以通过重新布线,使得某些节点的路径代价减少。如果以整体的眼光看,并不是每一个重新布线的节点都会出现在最终生成的路径中,但在生成随机树的过程中,每一次的重布线都尽可能的为最终路径代价减小创造机会。
所以在具体实现上,我直接继承RRT类在父类的getNearest函数上进行重写即可:
1 | def getNearest(self, node_list: list, node: Node) -> Node: |
2.3 Informed RRT* 算法
前面提到 RRT 和 RRT* 都是在均匀地撒点然后不断优化路径,但这样工作量很大,所以 Informed RRT* 将采样的范围限定成了椭圆,只需要在有用的区域进行撒点。
所以在 RRT* 的基础上进行修改来实现 Informed RRT* 算法,这里主要改动的是generateRandomNode函数:
在当前的最佳路径代价小于无穷大时采用椭圆采样,通过椭圆变换将单位球内的随机点映射到椭圆内,之后进行边界检查,确保生成的随机节点在环境的边界内,保证路径的有效性。
如果当前最佳路径代价为无穷大时,即尚未找到任何有效路径时,依然采用 RRT 的随机采样方法。
1 | def generateRandomNode(self) -> Node: |
2.4 Dynamic RRT 算法
Dynamic RRT 的主要目的在随机分布障碍物的环境中规划可行路径,会根据环境特征或当前搜索情况动态调整节点扩展的步长,可以使算法在开阔区域快速扩展,在障碍物密集区域细致搜索,同时平衡收敛时间和路径长度。
要实现 Dynamic RRT 算法,需要在 RRT* 代码的基础上添加一个 adjustStep 函数来根据当前环境特征计算动态步长,根据路径上的障碍物密度来调整步长大小:
1 | def adjustStep(self, from_node: Node, to_node: Node) -> float: |
三、实验结果
关于地图绘制,这里不是实验的重点,所以我在开源社区中找到了地图绘制和路径显示的套件(附在参考文献中),使用这个套件来进行结果的显示。主要是 plot.py 和 env.py 类,在 env 定义地图和障碍物,然后使用 plot 进行地图、路径、过程的显示。修改地图障碍物:
1 | class Map(Env): |
启动 motion planning,切换以上几种算法进行计算显示结果,这里因为 Dynamic RRT 涉及动态步长的调整,这个过程不是很明显,所以最后我选择没有在报告上进行呈现,以下为三个算法的结果展示:
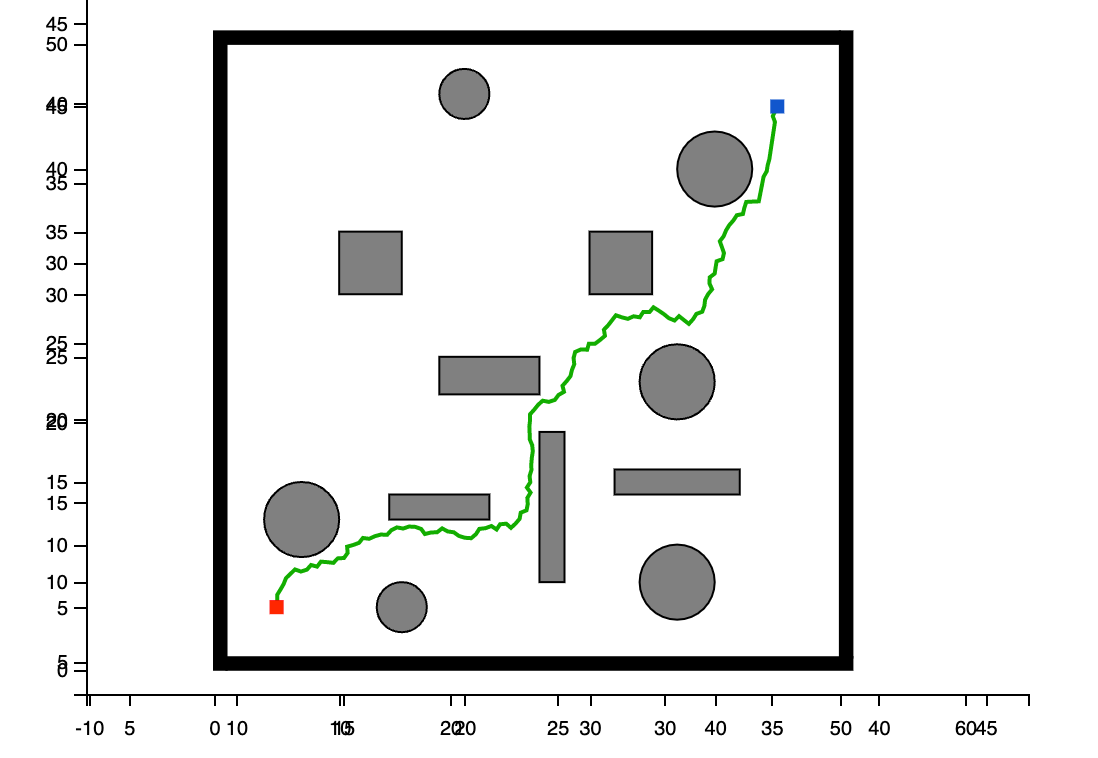
3.1 RRT算法
路径花费:72.31997074340283
用时:0.3871121406555176
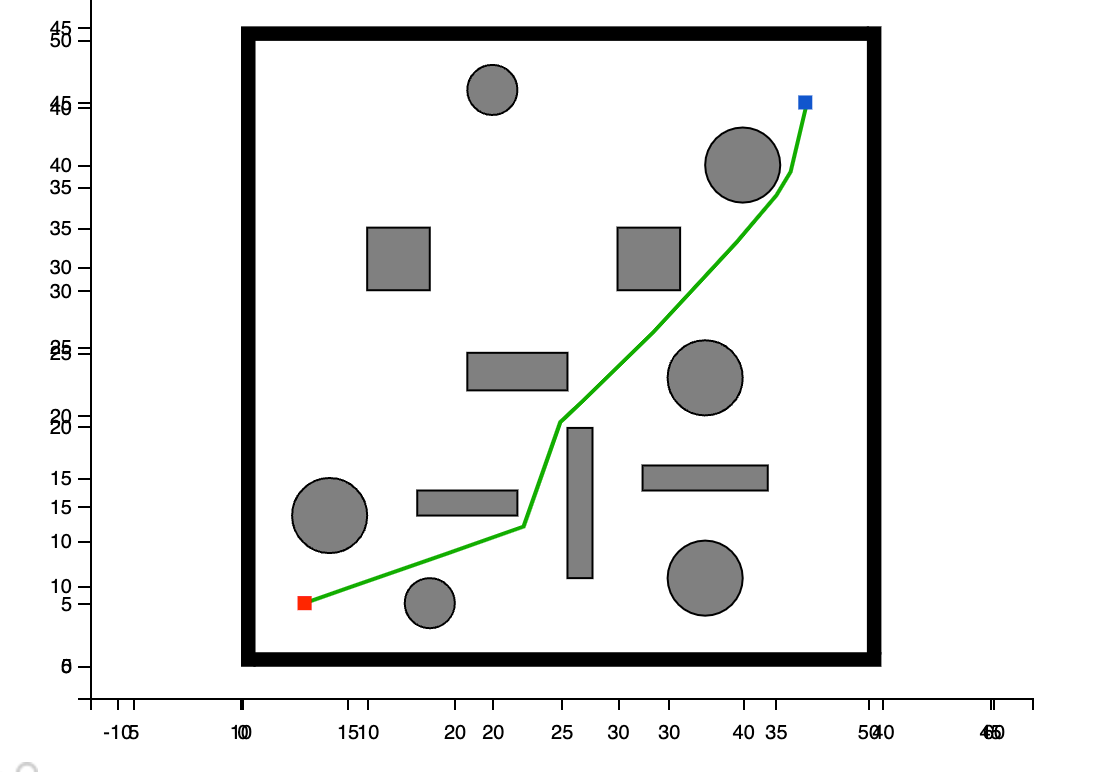
3.2 RRT* 算法
路径花费:60.31366129383614
用时:0.5569210052490234
可以看到加入重连步骤后,可以确保在的邻域范围得到的路径是最优的,所以相较于RRT算法得到的路径,RRT* 算法得到的路径更为平直。
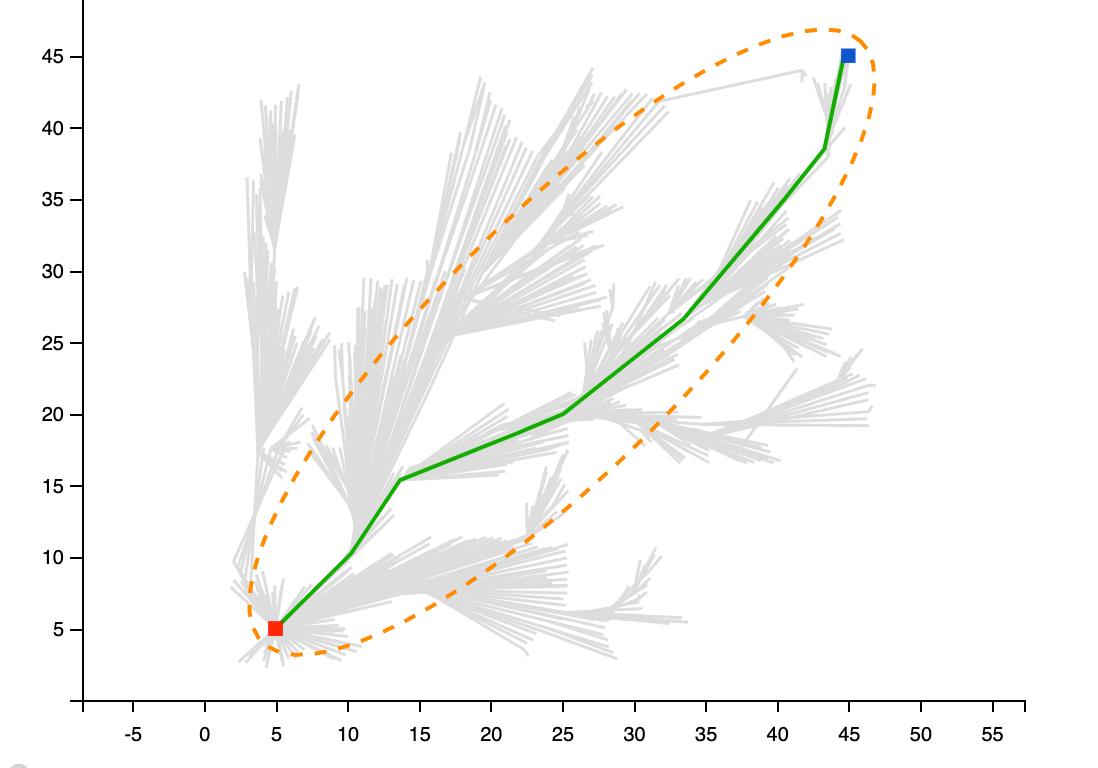
3.3 Informed RRT* 算法
路径花费:59.23146546218038
用时:0.15984631062490234
这里采用还是先前的地图,此时显示的是采样过程:
3.4 结果分析
对比这三个算法的结果,可以发现路径质量上,RRT 存在冗余转折,而 RRT* 通过优化已有路径,生成的路径质量比 RRT 更好些,Informed RRT* 引入椭圆采样进一步优化生成的路径质量更优。
而收敛速度上,RRT 计算成本相对较低,因为它只是简单地扩展树,RRT* 在 RRT 的基础上尝试优化路径,成本略大,但 Informed RRT* 又引入了启发式信息,加速了收敛。
本次实验在较小的规模中测试,具体的应用还是需要取决于具体的应用场景,需根据实际情况进行选择。
四、参考文献
- Connell, Devin and Hung Manh La. “Dynamic path planning and replanning for mobile robots using RRT.” 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (2017): 1429-1434.
- Yershova, A. & Jaillet, Léonard & Siméon, Thierry & LaValle, S.M.. (2005). Dynamic-Domain RRTs: Efficient Exploration by Controlling the Sampling Domain. 3856 - 3861. 10.1109/ROBOT.2005.1570709.
- Gammell J D , Srinivasa S S , Barfoot T D . Informed RRT*: Optimal Sampling-based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic[J]. 2014.
- 【路线显示参考】motion_planning/utils/plot/plot.py
- 【路径规划】RRT 算法求解最短路
- 【自动驾驶】基于采样的路径规划 RTT 算法
- 【路径规划】随机采样 Informed-RRT* 算法
- 【路径规划】动态RRT - Dynamic RRT